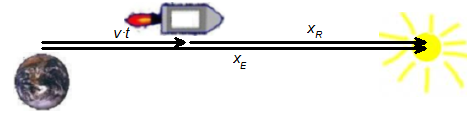
Eine Rakete fliegt mit der Geschwin- digkeit $v$ an der Erde vorbei.		Nach der Zeit $t$, in der die Rakete sich ein Stück von der Erde entfernt hat, messen ein Beobachter in der Rakete und ein Beobachter auf der Erde jeweils den Abstand $x$ zu einem Stern, auf den die Rakete zufliegt.

Anschließend berechnen beide aus ihren Werten, was der jeweils andere Beobachter gemessen hat.

Lösung klassisch:

Klassisch wäre die Lösung ganz einfach (siehe Bild oben):

relativistisch: Berechnung von $x_R$

Wir betrachten die Situation zunächst aus Sicht des Beobachters auf der Erde. Aufgrund der Zeitdilatation gilt dann: $\quad t_R = t_E\sqrt{1-\frac{v^2}{c^2}}\quad$.

Aus dem von dem Beobachter auf der Erde gemessenen Wert $x_E$ soll nun $x_R$ berechnet werden. Für den Beobachter auf der Erde ist die Zeit $t_E$ vergangen. Aus seiner Sicht hat die Rakete den Weg $v\cdot t_E$ zurückgelegt und ist noch $x_E - v\cdot t_E$ vom Stern entfernt (Das entspricht genau der klassischen Lösung oben). Da der Beobachter auf der Erde mit der Relativitätstheorie vertraut ist, weiß er, dass für den bewegten Beobachter in der Rakete die Strecke verkürzt ist (Längenkontraktion). Also rechnet er:

(Gleichung 1)

relativistisch: Berechnung von $x_E$

Aus Sicht des Beobachters in der Rakete bewegt sich die Erde: Sie fliegt „rückwärts”. Es gilt: $\quad t_E = t_R\sqrt{1-\frac{v^2}{c^2}}\quad$ (Zeitdilatation).

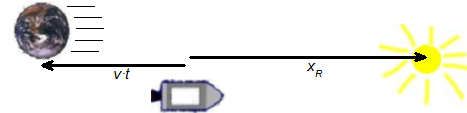
Aus dem von dem Beobachter in der Rakete gemessenen Wert $x_R$ soll nun $x_E$ berechnet werden. Für den Beobachter in der Rakete ist die Zeit $t_R$ vergangen. Die Erde hat in dieser Zeit den Weg $v\cdot t_R$ zurückgelegt und ist (aus Sicht der Rakete) $x_R + v\cdot t_R$ vom Stern entfernt. Aufgrund der Längenkontraktion erscheint die Strecke dem (bewegten) Beobachter auf der Erde allerdings verkürzt:

(Gleichung 2)

Lorentztransformation

Die physikalischen Überlegungen sind hiermit abgeschlossen. Mit ein paar mathematische Umformungen kann man die Gleichungen 1 und 2 nach $t_E$ und $t_R$ auflösen und erhält:

(Antoine, 30.3.)